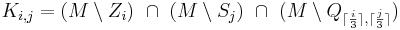Sie sind hier: Reiseführer > Freizeit_und_Spiele > Spiel > Sudoku

Sudoku

5	3
6
	9	8

	7
1	9	5



?	6

8
4
7

	6
8	?	3
	2

		3
		1
		6

	6


4	1

2	8
		5
	7

Sudoku ( jap. 数独 Sūdoku, kurz für 数字は独身に限る Sūji wa dokushin ni kagiru, wörtlich: Zahlen als Einzel beschränken) ist ein Zahlenpuzzle.

Inhaltsverzeichnis

1 Regeln und Begriffe
2 Ursprung
3 Lösungsmethoden
4 Erstellung neuer Sudokus
- 4.1 Algorithmus
5 Mathematik
6 Hilfen beim Lösen
7 Weblinks

Regeln und Begriffe

Das Puzzlespiel besteht meistens aus einem 9×9-Gitterfeld, das in 3×3 Unterquadrate bzw. Blöcke eingeteilt ist, die auch als „Regionen“ bezeichnet werden. Jedes Unterquadrat („Region“) ist wieder in 3×3 Felder eingeteilt. Das Gesamtquadrat enthält also 81 Felder in 9 Reihen und 9 Spalten.

In einige dieser Felder sind schon zu Beginn Ziffern 1 bis 9 eingetragen, die so genannten „Vorgaben“. Typischerweise sind 22 bis 36 Felder von 81 möglichen vorgegeben. Es gibt allerdings auch bekannte Kombinationen, in denen 17 Zahlen ein eindeutiges Sudoku bilden. Die minimale Anzahl Ziffern, die nötig ist, um ein eindeutiges Sudoku zu bilden ist nicht bekannt. Das Puzzle muss nun so vervollständigt werden, dass in jeder der 9 Zeilen, Spalten und Blöcke jede Ziffer von 1 bis 9 genau einmal auftritt. Da jede Zahl in jedem der drei genannten „Bereiche“ nur einmal auftritt, ist der diesen Umstand andeutende Name des Puzzlespiels „Einzelne Zahl“.

Wenn eine Zahl in einem Feld möglich ist, bezeichnet man sie als „Kandidat“. Die drei Bereiche (Reihe, Spalte, Block) werden zusammengefasst als „Einheiten“ bezeichnet.

Inzwischen gibt es auch Sudokus mit 4×4 Unterquadraten und somit 256 (=16×16) Feldern, in die 16 verschiedene Zahlen, Buchstaben oder Symbole verteilt werden. Ebenso sind 5×5 Sudokus denkbar, etc. Für Kinder gibt es Sudokus mit einer Kantenlänge von 2 pro Unterquadrat, also werden dort nur 4 Ziffern oder Bildsymbole benötigt. Eine weitere Variante sind Sudokus mit treppenförmiger Begrenzung der Blöcke (engl. Stairstep Sudoku).

Seit Ende 2005 gibt es tragbare, elektronische Sudoku-Geräte.

Ursprung

Der früheste Ursprung des Sudoku kann in den Rätselspielen des Schweizer Mathematikers Leonhard Euler gesehen werden, der solche unter dem Namen Carré latin ( Lateinisches Quadrat ) bereits im 18. Jahrhundert verfasste. Abweichend von den modernen Sudoku-Rätseln sind diese nicht in Blöcke (Unterquadrate) unterteilt.

Das heutige Sudoku in Blockform wurde 1979 in der Zeitschrift Math Puzzels & Logic Problems in den USA erstmals publiziert. Seinen Durchbruch erlangte das Sudoku jedoch erst um etwa 1984, als die japanische Zeitschrift Nikoli diese zunächst unter dem Namen Sūji wa dokushin ni kagiru regelmäßig abdruckte. Hieraus entwickelte sich schließlich der Begriff Sudoku. Der Neuseeländer Wayne Gould hat Sudoku auf einer Japanreise kennen gelernt. Sechs Jahre brauchte er, um eine Software zu entwickeln, die neue Sudokus per Knopfdruck entwickeln kann.

Anschließend bot er seine Rätsel der Times in London an. Die Tageszeitung druckte die ersten Sudoku-Rätsel und trat auf diese Weise eine Sudoku-Lawine in der westlichen Welt los. Inzwischen haben schätzungsweise 100 Millionen Menschen weltweit mindestens eine Partie Sudoku gespielt, heißt es.

In Österreich führte der regelmäßige Abdruck in Tageszeitungen wie Der Standard und Kronen Zeitung zu einer raschen Verbreitung Ende 2005. Des weiteren erscheint es regelmäßig in der Hersfelder Zeitung, der Frankfurter Rundschau, in Der Tagesspiegel und mittlerweile auch in der ZEIT.

Lösungsmethoden

Intuitiv

Lösungsansatz am oben abgebildeten Beispiel: Wenn man in das Unterquadrat rechts unten die 1 eintragen will, so legt die 1 in der Mitte der vorletzten Zeile fest, dass in dieser Zeile sonst keine 1 stehen darf. Ebenso scheidet die letzte Spalte aus, da dort weiter oben schon eine 1 steht. Die einzige verbleibende Möglichkeit ist also das freie Feld in der untersten Zeile dieses Unterquadrates.

Analytisch-systematisch

Abtastung

Abtastung (engl: Scanning) wird am Anfang und regelmäßig während der Lösung durchgeführt. Eventuell müssen „Scans“ mehrmals zwischen den Analyseperioden durchgeführt werden. Scanning besteht aus zwei grundlegenden Verfahren:

„Kreuzschraffur“ (Cross-hatching): die Abtastung der Reihen (oder Spalten), um zu erkennen, welche Linie bei der Überkreuzung in einer bestimmten Region eine bestimmte Zahl durch ein Verfahren der Eliminierung enthalten kann. Für die schnellsten Resultate werden die Zahlen in der Reihenfolge ihrer Häufigkeit abgesucht. Es ist wichtig, dieses Verfahren systematisch auf die Überprüfung alle Ziffer 1 bis 9 durchzuführen. (Illustration siehe )
„Auszählung“ der fehlenden Zahlen in den Einheiten (Counting numbers in units).

Analyse

Die zwei Hauptanalyseverfahren sind die Eliminierung (oder Kandidatenbeseitigung) und die Hypothese (oder „was-wenn“).

In der Eliminierung kommt man damit vorwärts, dass man mehrmals hintereinander Kandidatenzahlen von einer oder mehreren Zellen beseitigt, um gerade eine Wahl zu lassen. Nachdem jede Antwort erzielt wurde, wird zur Überprüfung noch ein üblicher „Scan“ durchgeführt, um die Auswirkung der neuesten Zahl zu sehen. Es gibt eine Vielzahl von Eliminierungstaktiken, die alle auf den einfachen oben genannten Regeln basieren, welche wichtige und nützliche logische Schlussfolgerungen beinhalten.
1. Durch Ausschluss:
  Man sucht die Spalte, Reihe oder das Unterquadrat (sog. „Block“ oder „Region“) mit den wenigsten Leerstellen heraus und notiert die fehlenden Ziffern auf einem separaten Blatt, um den Überblick zu behalten. In dem Sudoku der Abbildung z. B. die 5. Spalte. Hier fehlen 3, 4, 5, 8. Nun schreibt man mit Bleistift in die freien Felder alle möglichen Ziffern. In der 3. Reihe also 3 und 4. Da in der 5. Reihe direkt in der Mitte nur die 5 stehen kann, kann man in allen drei Einheiten die 5 streichen, so das in der 7. Reihe nur die 3, und folglich in der 3. Reihe, nachdem man die überzählige Zahl 3 gestrichen hat, die 4 stehen bleibt. Die Reihe ist komplett und man kann die korrekten Ziffern mit einer anderen Farbe oder mit Kugelschreiber fixieren. Dann wendet man sich der nächsten Einheit zu usw. Auf einfache Weise lassen sich alle Kästchen füllen. Je nach Anzahl der vorgegebenen Ziffern muss man zunächst eine Zeit lang in einer größeren oder kleineren Anzahl von Kästchen zwei oder mehrere Ziffern stehen lassen, ehe klar wird, welche Ziffer die richtige ist. Diese Technik ist die 1. und einfachste und gehört zu den „Scanning“-Methoden, sie wird auch „Nackter Einer“ (engl. „Nacked Single“) genannt.
2. Durch Kombination:
  Enthalten zwei Blöcke in einer Reihe die gleiche Ziffer (z. B. im obigen Beispiel die Ziffer 5 in dem Block oben links und oben Mitte), so kann die Position der Ziffer in dem dritten Block der Reihe oft direkt ermittelt werden: In dem dritten Block muss die Ziffer in der noch nicht mit der Ziffer belegten Reihe sein. Wenn nun für die Ziffer in dem dritten Block nur noch eine Spalte übrig bleibt – weil die anderen Felder der Reihe im Block 3 schon belegt sind oder die entsprechende Spalte in einem anderen Block die Ziffer schon enthält – so kann die Ziffer sofort eingetragen werden. Das Gleiche gilt analog für Spalten. Im Beispiel oben wird so schnell klar, dass Ziffer 5 in dem rechten oberen Block in der linken unteren (grün hervorgehobenen) Zelle stehen muss. Dies ist die zweite Technik und gehört zu der einfachen Gruppe der „Scanning“-Methoden, sie wird „Versteckter Einer“ (engl. „Hidden Single“) genannt. (Illustration siehe , Scanning-Methode)

Algorithmisch

Eine Methode zum Lösen eines Sudoku ist die Behandlung als Schnittmengenproblem . Aus den vorgegebenen Ziffern lässt sich für jedes Feld eine Menge von Kandidatenziffern bestimmen, die für ein Feld die Schnittmenge aus je drei Mengen ist: Diese sind die Komplemente der jeweils in der selben Zeile, Spalte und im selben Quadrat enthaltenen Ziffern zur Menge aller Ziffern (ohne die Null). In einfachen Fällen hat das Rätsel die Eigenschaft, dass mindestens ein Feld eine einelementige Kandidatenmenge besitzt, oder dass ein Element aus einer Kandidatenmenge eines Feldes nicht in den Kandidatenmengen aller anderen Felder der selben Spalte oder Zeile oder des selben Quadrats vorkommt. Dieser Kandidat kann dann fest in das jeweilige Feld eingesetzt werden und die betreffende Ziffer aus den Kandidatenmengen der übrigen Felder in der selben Zeile, Spalte und im selben Quadrat entfernt werden. Dieses Verfahren wird dann solange wiederholt, bis alle Zellen aufgefüllt sind.

$M = \{ 1 \cdots 9\}$ Ziffern
$Z_1 \cdots Z_9$ Mengen der in je einer Zeile enthaltenen Ziffern
$S_1 \cdots S_9$ Mengen der in je einer Spalte enthaltenen Ziffern
$Q_{1,1} \cdots Q_{3,3}$ Mengen der je in einem Teilquadrat enthaltenen Ziffern

Die Kandidatenmenge $K i, j$ eines Feldes $F i, j$ berechnet sich dann in jedem Iterationsschritt wie folgt:

$K_{i,j} = (M \setminus Z_i) \ \cap \ (M \setminus S_j) \ \cap \ (M \setminus Q_{ \lceil \frac{i}{3} \rceil , \lceil \frac{j}{3} \rceil })$

Bei den meisten eindeutig lösbaren Rätseln, insbesondere den schwierigen, führt diese Methode allein nicht zur Lösung. In diesen Fällen müssen z. B. Paare oder Tripel von Kandidaten gemeinsam betrachtet werden, um die Kandidatenmengen in einem ersten Schritt zu verkleinern. Hierbei werden logische Verknüpfungen zwischen mehreren Feldern gesucht, von denen klar ist, dass bestimmte Zahlen in den Feldern dieser Gruppe stehen, wodurch diese Zahlen für die nicht in der Gruppe befindliche als Lösungen ausscheiden (Beispiel: {1, 2} {2, 3} {3, 1}; wenn diese Kanditatenmengen z. B. in einer Reihe stehen, ist klar, dass diese Gruppe die Zahlen 1, 2 und 3 enthalten muss, wodurch sie aus allen anderen Kandidatenmengen in dieser Reihe ausscheiden). Alternativ kann, falls in einem Iterationsschritt keine einelementige Kandidatenmenge existiert, aus einer der (kleinsten) Kandidatenmengen eine Zahl ausgewählt werden, um eine der mehreren möglichen Lösungen zu erhalten (Versuch-und-Irrtum-Methode).

Nach der Backtracking-Methode

Auf dem Computer kann man ein Sudoku mit der Backtracking -Methode lösen. Beginnend mit dem ersten freien Feld, probiert man systematisch, mit der Eins beginnend, ob man zu einer Lösung kommt. Beim ersten Widerspruch geht man zurück (engl. backtrack). Dieser Lösungsweg lässt sich sehr elegant rekursiv formulieren, und man ist sicher, dass alle Kombinationsmöglichkeiten abgesucht werden. Da es sich um tausende Wege handeln kann, ist dieser Algorithmus nur für Computerprogramme geeignet. Der Lösungsalgorithmus ist sicher nur suboptimal , da er keinerlei analytische Vorinformationen verwendet und nur durch Ausprobieren vorgeht. Dennoch erhält man auf gewöhnlichen PCs die Lösung innerhalb einer Sekunde.

Erstellung neuer Sudokus

Schwieriger als das Lösen der Puzzle dürfte das Herstellen sein.

Eindeutige Lösung: Es soll nur eine korrekte Lösung existieren.
Gewünschter Schwierigkeitsgrad: Die Anzahl der vorgegebenen Ziffern bestimmt nicht allein den Schwierigkeitsgrad. Die Anordnung spielt eine entscheidende Rolle.

Algorithmus

Belegung des gelösten Puzzles erstellen
- 1. Weg: Ein leeres Puzzlefeld wird Zelle für Zelle durch „Auswürfeln“ ( Zufallsgenerator ) mit Ziffern befüllt. Sobald es zu einem Regelverstoß kommt, muss per Backtracking -Methode eine andere Belegung probiert werden. Dies ist weniger trivial als beim Lösen des Puzzles: Da eine möglichst „zufällige“ Belegung des Puzzlefeldes benötigt wird, kann man nicht einfach alle Ziffern der Reihe nach durchprobieren. Es hindert aber nicht, alle Ziffern, sobald sie einmal „ausgewürfelt“ wurden, als künftig – für die jeweilige Zelle – gesperrt „abzuhaken“ (in einer Tabelle zu markieren)
- 2. Weg: Neun Einsen ohne Regelverstoß im Puzzelfeld verteilen. Dann neun Zweier, neun Dreier, usw. verteilen. Auch hier muss ein Backtracking -Algorithmus angewandt werden.
- 3. Weg: Man füllt eine Zeile oder eine Spalte in beliebiger Reihenfolge mit den erlaubten Ziffern, verschiebt dann mit jeder weiteren Zeile/Spalte die Ziffernfolge, bis man am Schluss alle möglichen Varianten untereinander/nebeneinander in einer n×n-Matrix vorliegen hat. Dies alleine wäre ein äußerst trivial zu lösendes Rätsel, da sich die Ziffernfolgen wiederholen; deswegen sollte man über erlaubte Transformationen diese Matrix nun schrittweise so verändern, dass die Ursprungsziffernfolge sowie die ausgeführten Transformationen nicht mehr nachvollziehbar sind. Erlaubte Transformationen sind z. B. das Invertieren, das Spiegeln (vertikal, horizontal, schräg), Rotieren, Vertauschen ganzer Zeilen oder Spalten, sofern sie innerhalb eines Mini-Quadrates bleiben, oder das Vertauschen ganzer Zeilen und Spalten von Miniquadraten. Etliche dieser Transformationen hintereinander verwischen (fast) alle Hinweise auf die ursprüngliche Ziffernfolge. Von den hier vorgestellten Erstellungsmethoden ist diese die am wenigsten aufwendige und rechenintensive.
Zur Lösung passendes Sudoku-Rätsel erzeugen
- Wiederum durch „Auswürfeln“ werden je nach Schwierigkeitsgrad zwischen 45 und 57 Ziffern wieder entfernt. Ohne weitere Kontrolle kann es hierbei passieren, dass das Puzzle trivial (langweilig) oder nicht mehr eindeutig lösbar wird.

Mathematik

Die Zahl der möglichen 9×9-Sudokus beträgt nach Berechnung von Bertram Felgenhauer (im Jahr 2005) 6,67090375202107293696 · 10²¹ ; diese Zahl ist gleich 9! · 72² · 2⁷ · 27.704.267.971; der letzte Faktor ist eine Primzahl . Die Zahl wurde unabhängig davon durch Ed Russell bestätigt. Nach Ed Russell und Frazer Jarvis gibt es 5.472.730.538 Möglichkeiten bei Berücksichtigung von Symmetrien. Die Zahl gültiger 16×16-Sudokus ist unbekannt.

Die maximale Zahl von Vorgaben, die nicht zu einer eindeutigen Lösung führen, ist, unabhängig von der Variante, um vier geringer als die Gesamtzahl der Felder (z. B. 81 - 4 = 77 bei der Standardvariante). Wenn von zwei Zahlen jeweils zwei Vorgaben fehlen, die zugehörigen Felder auf den Ecken eines Rechtecks liegen, dessen Ecken paarweise im selben Block liegen und dessen Kanten in der selben Zeile bzw. Spalte liegen, gibt es zwei Möglichkeiten, diese Zahlen einzutragen. Das andere Extrem – die Mindestzahl von Vorgaben, die zu einer eindeutigen Lösung führen – zu bestimmen ist ein ungelöstes Problem. Die Mindestzahl, die bisher für die Standardvariante ohne Symmetrieforderung gefunden wurde, ist 17. Dies haben japanische Rätselenthusiasten herausgefunden. Bei drehsymmetrischer Anordnung sind es 18.

Hilfen beim Lösen

Die Hilfen zum Lösen eines Sudokus sind nicht normiert. Deshalb werden hier nur Hilfen angeboten, die jeder individuell abändern und verfeinern kann.

Die „Uhrzeigerstrichmethode“

Da die Sudokus in Zeitungen und Magazinen häufig sehr klein abgedruckt sind, ist die Uhrzeigerstrichmethode hilfreich, die Kandidaten für ein Feld festzuhalten. Man macht im Feld einen kleinen Strich an der Stelle des „Uhrzeigers“ (siehe Bild). Die Fünf stellt eine Ausnahme dar; sie wird als kleiner Punkt in der Mitte dargestellt. So kann man sich mehrere Kandidaten für ein Feld merken. Wenn man keinen Radiergummi zur Hand hat, kann man einen Kandidatenstrich einfach durchstreichen, wenn weitere Überlegungen diesen ausschließen. Diese Methode ist bei weitem leserlicher als das Schreiben von kleinen Zahlen.

Unsichere Zahlen markieren

„Zahlen trage ich nur mit Bleistift ein, um sie notfalls wieder wegradieren zu können. Eine unsichere Zahl markiere ich mit einem Sternchen, alle nachfolgenden dann mit einem Punkt. Taucht später ein Fehler auf, kann ich alle markierten Zahlen wegradieren und an der Sternchen-Stelle neu ansetzen“, empfiehlt Kerstin Wöge aus Spandau, die erste Deutsche Sudoku-Meisterin, in der BZ vom 29. November 2005.

Papierstreifen

Man kann sich auch zwei bis drei Papierstreifen zuschneiden. Mit diesen kann man gleiche Zahlen abdecken. Am besten geht man die Zahlenreihe immer wieder von 1 bis 9 durch. Das erleichtert das Ausfüllen ungemein, da man vom Zahlengewirr nicht abgelenkt wird.

Das „Negativraster“

Durch ein Rastern der leeren Felder in neun Hilfsfelder (kann man real aber auch bloß im Kopf ausführen) lassen sich durch systematisches Ankreuzen der nicht möglichen Zahlen sowohl Fehler vermeiden als auch bei einfacheren Rätseln sogar direkt richtige Zahlen finden. Diese Hilfsmethode wird auf einer psychologischen Website im Detail beschrieben und an Hand eines Beispiels erklärt. Dort wird auch darauf hingewiesen, dass diese Rätselform sowohl das logische Denken als auch die Konzentrationsfähigkeit fördert.

Weblinks

Sudoku-Spiele in "Die Zeit" - Online-Spiele in verschiedenen Schwierigkeitsgraden
Sudoku als Brettspiel - Übersichtsartikel der Zeitschrift Spielbox
Lösungsanleitung (englisch) (PDF)
Java-Offline-Sudoku (Spiel, Generator, Hilfe und Löser)
Javascript Sudoku Hilfe und Löser - Plattformunabhängige Unterstützung beim Lösen von Sudokus

Kategorie : Spiel

Wikipedia

Dieser Artikel basiert auf dem Artikel Sudoku aus der freien Enzyklopädie Wikipedia und steht unter der GNU-Lizenz für freie Dokumentation . In der Wikipedia ist eine Liste der Autoren des Artikels Sudoku verfügbar.